$\LaTeX{}$ 之数学公式（四）

发表于 更新于 分类于 ， 本文字数： 6.5k 阅读时长 ≈ 24 分钟

本文主体内容来自一份 (不太) 简短的 LATEX2ε 介绍。

本章将见识到 \(\LaTeX{}\) 闻名的强项——排版数学公式。

\(\textrm{AMS}\) 宏集

在介绍数学公式排版之前，简单介绍一下 \(\textrm{AMS}\) 宏集。\(\textrm{AMS}\) 宏集合是美国数学学会(American Mathematical Society)提供的对\(\LaTeX{}\) 原生的数学公式排版的扩展，其核心是 amsmath 宏包，对多行公式的排版提供了有力的支持。此外，amsfonts 宏包以及基于它的 amssymb 宏包提供了丰富的数学符号；amsthm 宏包扩展了 \(\LaTeX{}\) 定理证明格式。

以下示例都假定了导言区中写有 \usepackage{amsmath} 。

公式排版基础

行内和行间公式

数学公式有两种排版方式：其一是与文字混排，称为行内公式；其二是单独列为一行排版，称为行间公式。

行内公式由一对 \(\texttt\$\) 符号包裹：The Pythagorean theorem is \(a^2 + b^2 = c^2\) ($a^2 + b^2 = c^2$)。

单独成行的行间公式由 \(\texttt{equation}\) 环境包裹。 \(\texttt{equation}\) 环境为公式自动生成一个编号，这个编号可以用\label 和 \ref 生成交叉引用，amsmath 的 \eqref 命令甚至为引用自动加上圆括号；还可以用\tag 命令手动修改公式的编号，或者用\notag 命令取消为公式编号（与之基本等效的命令是 \nonumber）。

image-20250116220746833

image-20250116220821758

1
2
3
\begin{equation}
1 + 1 = 3 \tag{dumb}
\end{equation}
1
2
3
\begin{equation}
1 + 1 = 4 \notag
\end{equation}

\[ \begin{equation} 1 + 1 = 3 \tag{dumb} \end{equation} \]

\[ \begin{equation} 1 + 1 = 4 \notag \end{equation} \]

如果需要直接使用不带编号的行间公式，则将公式用命令 \[ 和 \] 包裹，与之等效的是 \(\texttt{displaymath}\) 环境。有的人更喜欢 \(\texttt{equation*}\) 环境，体现了带星号和不带星号的环境之间的区别。

image-20250116221231100

通过一个例子展示行内公式和行间公式的对比。为了与文字相适应，行内公式在排版大的公式元素（分式、巨算符等）时显得很“局促”：

image-20250116221343609

行间公式的对齐、编号位置等性质由文档类选项控制，文档类的 \(\texttt{fleqn}\) 选项令行间公式左对齐；\(\texttt{leqno}\) 选项令编号放在公式左边。

数学模式

当用户使用 \(\texttt\$\) 开启行内公式输入，或是使用 \[ 命令、\(\texttt{equation}\) 环境时，\(\LaTeX{}\) 就进入了数学模式。

数学模式相比于文本模式有以下特点：

  1. 数学模式中输入的空格被忽略。数学符号的间距默认由符号的性质（关系符号、运算符等）决定。需要人为引入间距时，\quad 和 \qquad 等命令。
  2. 不允许有空行（分段）。行间公式中也无法用 \\命令手动换行。
  3. 所有的字母被当作数学公式中的变量处理，字母间距与文本模式不一致，也无法生成单词之间的空格。如果想在数学公式中输入正体的文本，简单情况下可用 \mathrm 命令。或者用 \amsmath 提供的 \text 命令。
1
2
3
$x^{2}  \geq 0 \qquad
\text{for \textbf{all} }
x\in \mathbb{R}$

\[ \begin{gather*} x^{2} \geq 0 \qquad \text{for \textbf{all} } x\in \mathbb{R} \end{gather*} \]

数学符号

\(\LaTeX{}\)​ 默认提供了常用的数学符号，amssymb 宏包提供了一些次常用的符号。大多数常用的数学符号都能在 这里 查到。更多符号可在命令行输入texdoc symbols-a4 查阅 。

一般符号

希腊字母符号的名称就是其英文名称，如 \(\alpha\) (\alpha)、\(\beta\) (\beta)等等。大写的希腊字母为首字母大写的命令 \(\Gamma\) (\Gamma) \(\Delta\) (\Delta)。无穷大符号为 \(\infty\) (\infty)。

省略号有 \(\dots\) (\dots) 和 \(\cdots\) (\cdots) 两种形式。它们有各自合适的用途：

1
2
$a_1, a_2, \dots, a_n$ \\
$a_1 + a_2 + \cdots + a_n$

\[ \begin{gather*} a_1, a_2, \dots, a_n \\ a_1 + a_2 + \cdots + a_n \end{gather*} \]

\ldots 和 \dots 是完全等效的，它们既能用在公式中，也用来在文本里作为省略号。 除此之外，在矩阵中可能会用到竖排的 \(\vdots\) (\votes)和斜排的 \(\ddots\) (\ddots)。

指数、上下标和导数

用^ 和 _标明上下标。注意上下标的内容（子公式）一般需要用花括号包裹，否则上下标只对后面的一个符号起作用。

1
2
3
4
5
$p^3_{ij} \qquad
m_\mathrm{Knuth}\qquad
\sum_{k=1}^3 k $\\[5pt]
$a^x+y \neq a^{x+y}\qquad
e^{x^2} \neq {e^x}^2$

\[ \begin{gather*} p^3_{ij} \qquad m_\mathrm{Knuth}\qquad \sum_{k=1}^3 k \\[5pt] a^x+y \neq a^{x+y}\qquad e^{x^2} \neq {e^x}^2 \end{gather*} \]

导数符号'(\({}'\))是一类特殊的上标，可连续使用，但只能在其后添加其他上标：

1
$f(x) = x^2 \quad f'(x) = 2x \quad f''^{2}(x) = 4$

\[ f(x) = x^2 \quad f'(x) = 2x \quad f''^{2}(x) = 4 \]

分式和根式

分式使用 \frac{分子}{分母} 来书写。分式的大小在行间公式中是正常大小，而在行内被极度压缩。 amsmath 提供了方便的命令 \dfrac 和 \tfrac，令用户能够在行内使用正常大小的分式，或是反过来。

1
2
3
4
5
6
7
8
In display style:
\[
3/8 \qquad \frac{3}{8}
\qquad \tfrac{3}{8}
\]
In text style:
$1\frac{1}{2}$~hours \qquad
$1\dfrac{1}{2}$~hours

image-20250118195233817

一般的根式使用 \sqrt{...}；表示 \(n\) 次方根时写成 \sqrt[n]{...}。

1
2
3
$\sqrt{x} \Leftrightarrow x^{1/2}
\quad \sqrt[3]{2}
\quad \sqrt{x^{2} + \sqrt{y}}$

\[ \sqrt{x} \Leftrightarrow x^{1/2} \quad \sqrt[3]{2} \quad \sqrt{x^{2} + \sqrt{y}} \]

特殊的分式形式，如二项式结构，由 amsmath 宏包的 \binom 命令生成：

1
2
3
4
\[
\binom{n}{k} =\binom{n-1}{k}
+ \binom{n-1}{k-1}
\]

\[ \binom{n}{k} =\binom{n-1}{k} + \binom{n-1}{k-1} \]

关系符

常见的关系符号除了可以直接输入的 \(=\)，\(>\)，\(<\)，其它符号用命令输入，常用的有 \(\ne\) (\ne)、\(\ge\) (\ge)、\(\le\) (\le)、\(\approx\) （\approx）、 等价 \(\equiv\) (\equiv)、正比 \(\propto\) (\propto)、相似 \(\sim\)\sim 等等。

\(\LaTeX{}\) 还提供了自定义二元关系符的命令 \stackrel，用于将一个符号叠加在原有的二元关系符之上：

1
$f_n(x) \stackrel{*}{\approx} 1$

\[ f_n(x) \stackrel{*}{\approx} 1 \]

运算符

\(\LaTeX{}\) 中的算符大多数是二元算符，除了直接用键盘可以输入的 \(+\)、\(-\)、\(*\)、\(/\)，其它符号用命令输入，常用的有乘号 \(\times\) (\times)、 除号 \(÷\)（\div）、点乘 \(\cdot\) (\cdot)、加减号\(\pm\) (\pm) / \(\mp\) (\mp)等等。

\(\nabla\) (\nabla) 和 \(\partial\) (\partial) 也是常用的算符，虽然它们不属于二元算符。

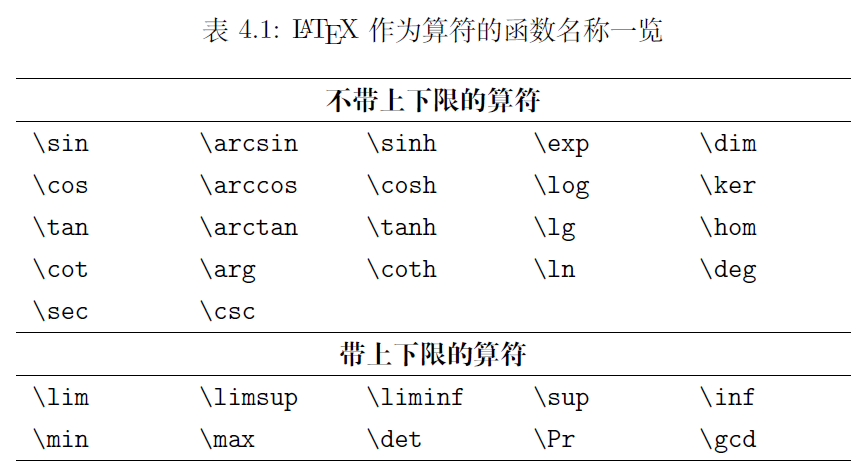
\(\LaTeX{}\) 将数学函数的名称作为一个算符排版，字体为直立字体。其中有一部分符号在上下位置可以书写一些内容作为条件， 类似于后文所叙述的巨算符。

image-20250118202405498

1
$\lim_{x \rightarrow 0} \frac{\sin x}{x} = 1$

\[ \lim_{x \rightarrow 0} \frac{\sin x}{x} = 1 \]

对于求模表达式，\(\LaTeX{}\) 提供了 \bmod和 \pmod 命令，前者相当于一个二元运算符，后者作为同余表达式的后缀：

1
2
$a\bmod b \\
 x\equiv a \pmod{b}$

\[ \begin{gather*} a\bmod b \\ x\equiv a \pmod{b} \end{gather*} \]

如果上表中的算符不够用的话，amsmath 允许用户在导言区用 \DeclareMathOperator定义自己的算符，其中带星号的命令定义带上下限的算符：

1
2
3
4
\DeclareMathOperator{\argh}{argh}
\DeclareMathOperator*{\nut}{Nut}

\[\argh 3 = \nut_{x=1} 4x\]

\[ \DeclareMathOperator{\argh}{argh} \DeclareMathOperator*{\nut}{Nut} \argh 3 = \nut_{x=1} 4x \]

巨算符

积分号 \(\int\) (\int)、求和号 \(\sum\) (\sum) 等符号称为巨算符。巨算符在行内公式和行间公式的大小和形状有区别。行内:\(\sum_{i=1}^n \quad \int_0^{\frac{\pi}{2}} \quad \oint_0^{\frac{\pi}{2}} \quad \prod_\epsilon\) ，行间：

1
2
3
4
\[\sum_{i=1}^n \quad
\int_0^{\frac{\pi}{2}} \quad
\oint_0^{\frac{\pi}{2}} \quad
\prod_\epsilon \]

\[ \sum_{i=1}^n \quad \int_0^{\frac{\pi}{2}} \quad \oint_0^{\frac{\pi}{2}} \quad \prod_\epsilon \]

巨算符的上下标位置可由 \limits 和 \nolimits调整，前者令巨算符类似 \(\lim\) 或求和算符 \(\sum\)，上下标位于上下方；后者令巨算符类似积分号，上下标位于右上方和右下方。行内:\(\sum\limits_{i=1}^n \quad \int\limits_0^{\frac{\pi}{2}} \quad \prod\limits_\epsilon\) ; 行间:

1
2
3
\[\sum\nolimits_{i=1}^n \quad
\int\limits_0^{\frac{\pi}{2}} \quad
\prod\nolimits_\epsilon \]

\[ \sum\nolimits_{i=1}^n \quad \int\limits_0^{\frac{\pi}{2}} \quad \prod\nolimits_\epsilon \]

amsmath 宏包还提供了 \substack，能够在下限位置书写多行表达式；\(\texttt{subarray}\) 环境更进一步，令多行表达式可选择居中 (c) 或左对齐 (l)：

1
2
3
4
5
6
7
8
9
10
11
12
% \usepackage{amssymb}
\[
\sum_{\substack{0\le i\le n \\
  j\in \mathbb{R}}}
P(i,j) = Q(n)
 \\
\sum_{\begin{subarray}{l}
  0\le i\le n \\
  j\in \mathbb{R}
\end{subarray}}
P(i,j) = Q(n)
\]

\[ \begin{gather*} \sum_{\substack{0\le i\le n \\ j\in \mathbb{R}}} P(i,j) = Q(n) \\ \sum_{\begin{subarray}{l} 0\le i\le n \\ j\in \mathbb{R} \end{subarray}} P(i,j) = Q(n) \end{gather*} \]

数学重音和上下括号

数学符号可以像文字一样加重音，比如求导符号 \(\dot{r}\) （\dot{r}）、 \(\ddot{r}\) (\ddot{r})、表示向量的箭头 \(\vec{r}\) (\vec{r}) 、表示单位向量的符号 \(\hat{\mathbf{e}}\) (\hat{mathbf{e}})等。使用时要注意重音符号的作用区域，一般应当对某个符号而不是“符号加下标”使用重音：

1
2
3
4
$\bar{x_0} \quad \bar{x}_0$\\[5pt]
$\vec{x_0} \quad \vec{x}_0$\\[5pt]
$\hat{\mathbf{e}_x} \quad
 \hat{\mathbf{e}}_x$

\[ \begin{gather*} \bar{x_0} \quad \bar{x}_0\\[5pt] \vec{x_0} \quad \vec{x}_0\\[5pt] \hat{\mathbf{e}_x} \quad \hat{\mathbf{e}}_x \end{gather*} \]

也能为多个字符加重音，包括直接画线的 \overline 和 \underline 命令（可叠加使用）、宽重音符号 \widehat、表示向量的箭头 \overrightarrow 等。

1
2
3
$0.\overline{3} = \underline{\underline{1/3}}$ \\[5pt]
$\hat{XY} \qquad \widehat{XY}$\\[5pt]
$\vec{AB} \qquad \overrightarrow{AB}$

\[ \begin{gather*} 0.\overline{3} = \underline{\underline{1/3}} \\[5pt] \hat{XY} \qquad \widehat{XY}\\[5pt] \vec{AB} \qquad \overrightarrow{AB} \end{gather*} \]

\overbrace 和 \underbrace 命令用来生成上/下括号，各自可带一个上/下标公式。

1
2
3
$\underbrace{\overbrace{(a+b+c)}^6
\cdot \overbrace{(d+e+f)}^7}
_\text{meaning of life} = 42$

\[ \underbrace{\overbrace{(a+b+c)}^6 \cdot \overbrace{(d+e+f)}^7} _\text{meaning of life} = 42 \]

箭头

常用的箭头包括 \rightarrow(\(\rightarrow\)，或 \to)、\leftarrow（\(\leftarrow\)，或\gets）等。

amsmath 的 xleftarrow 和 xrightarrow 命令提供了长度可以伸展的箭头，并且可以为箭头增加上下标：

1
2
\[ a\xleftarrow{x+y+z} b \] \\
\[ c\xrightarrow[x<y]{a*b*c}d \]

\[ \begin{gather*} a\xleftarrow{x+y+z} b \\ c\xrightarrow[x<y]{a*b*c}d \end{gather*} \]

括号和定界符

\(\LaTeX{}\) 提供了多种括号和定界符表示公式块的边界，如小括号 \(()\)、中括号 \([]\)、大括号 \(\{\}\) (\{ \})、尖括号 \(\langle \rangle\)（\langle \rangle）等。

1
${a,b,c} \neq \{a,b,c\}$

\[ {a,b,c} \neq \{a,b,c\} \]

使用 \left 和 \right 命令可令括号（定界符）的大小可变，在行间公式中常用。会自动根据括号内的公式大小决定定界符大小。 \left 和 \right 必须成对使用。需要使用单个定界符时，另一个定界符写成 \left. 或\right.。

1
2
3
4
\[1 + \left(\frac{1}{1-x^{2}}
\right)^3 \qquad
\left.\frac{\partial f}{\partial t}
\right|_{t=0}\]

\[ 1 + \left(\frac{1}{1-x^{2}} \right)^3 \qquad \left.\frac{\partial f}{\partial t} \right|_{t=0} \]

有时我们不满意于 \(\LaTeX{}\) 自动调节的定界符大小。这时还可以用 \big、bigg 等命令生成固定大小的定界符。 更常用的形式是类似 \left 的 \bigl、\biggl 等，以及类似 \right 的 \bigr、\biggr 等（\bigl 和 \bigr 不必成对出现）。

1
2
3
4
5
6
$\Bigl((x+1)(x-1)\Bigr)^{2}$\\
$\bigl( \Bigl( \biggl( \Biggl( \quad
\bigr\} \Bigr\} \biggr\} \Biggr\} \quad
\big\| \Big\| \bigg\| \Bigg\| \quad
\big\Downarrow \Big\Downarrow
\bigg\Downarrow \Bigg\Downarrow$

\[ \begin{gather*} \Bigl((x+1)(x-1)\Bigr)^{2}\\ \bigl( \Bigl( \biggl( \Biggl( \quad \bigr\} \Bigr\} \biggr\} \Biggr\} \quad \big\| \Big\| \bigg\| \Bigg\| \quad \big\Downarrow \Big\Downarrow \bigg\Downarrow \Bigg\Downarrow \end{gather*} \]

使用 \big 和 \bigg 等命令的另外一个好处是：用\left 和 \right 分界符包裹的公式块是不允许断行的（下文提到的 \(\texttt{array}\) 或者 \(\texttt{aligned}\) 等环境视为一个公式块），所以也不允许在多行公式里跨行使用，而 \big 和 \bigg 等命令不受限制。

多行公式

长公式折行

通常来讲应当避免写出超过一行而需要折行的长公式。如果一定要折行的话，习惯上优先在等号之前折行，其次在加号、减号之前，再次在乘号、除号之前。 其它位置应当避免折行。

amsmath 宏包的 \(\texttt{multline}\) 环境提供了书写折行长公式的方便环境。它允许用 \\ 折行，将公式编号放在最后一行。多行公式的首行左对齐，末行右对齐，其余行居中。

1
2
3
4
5
6
7
\begin{multline}
a + b + c + d + e + f
+ g + h + i \\
= j + k + l + m + n\\
= o + p + q + r + s\\
= t + u + v + x + z
\end{multline}

image-20250120103429233

与表格不同的是，公式的最后一行不写 \\，如果写了，反倒会产生一个多余的空行。

类似 \(\texttt{equation*}\)，\(\texttt{multline*}\) 环境排版不带编号的折行长公式。

多行公式

更多的情况是，需要罗列一系列公式，并令其按照等号对齐。 目前最常用的是 \(\texttt{align}\) 环境，它将公式用 \(\texttt\&\) 隔为两部分并对齐。分隔符通常放在等号左边：

1
2
3
4
\begin{align}
a & = b + c \\
& = d + e
\end{align}

\[ \begin{align} a & = b + c \\ & = d + e \end{align} \]

\(\texttt{align}\) 环境会给每行公式都编号。仍然可以用 \notag 去掉某行的编号。 在以下的例子，为了对齐等号，将分隔符放在右侧，并且此时需要在等号后添加一对括号 \(\texttt\{\texttt\}\) 以产生正常的间距：

1
2
3
4
5
6
\begin{align}
a ={} & b + c \\
  ={} & d + e + f + g + h + i + j + k + l \notag \\
            & + m + n + o \\
    ={} & p + q + r + s
\end{align}

\[ \begin{align} a ={} & b + c \\ ={} & d + e + f + g + h + i + j + k + l \notag \\ & + m + n + o \\ ={} & p + q + r + s \end{align} \]

\(\texttt{align}\) 还能够对齐多组公式，除等号前的 & 之外, 公式之间也用 & 分隔：

1
2
3
4
\begin{align}
a &=1  &  b &=2   & c &=3   \\
d &=-1 &  e &=-2  & f &=-5
\end{align}

\[ \begin{align} a &=1 & b &=2 & c &=3 \\ d &=-1 & e &=-2 & f &=-5 \end{align} \]

如果不需要按等号对齐，只需罗列数个公式，\(\texttt{gather}\) 将是一个很好用的环境：

1
2
3
4
5
6
\begin{gather}
a = b + c \\
d = e + f + g \\
h + i = j + k \notag \\
l + m = n
\end{gather}

\[ \begin{gather} a = b + c \\ d = e + f + g \\ h + i = j + k \notag \\ l + m = n \end{gather} \]

有对应的不带编号的版本 \(\texttt{align*}\)和 \(\texttt{gather*}\)。

公用编号的多行公式

另一个常见的需求是将多个公式组在一起公用一个编号，编号位于公式的居中位置。为此，amsmath 宏包提供了诸如 \(\texttt{aligned}\)、\(\texttt{gathered}\) 等环境，与 \(\texttt{equation}\) 环境套用。以 \(\texttt{-ed}\) 结尾的环境用法与前一节不以 \(\texttt{-ed}\) 结尾的环境用法一一对应。仅以 \(\texttt{aligned}\) 举例：

1
2
3
4
5
6
7
8
\begin{equation}
\begin{aligned}
a &= b + c \\
d &= e + f + g \\
h + i &= j + k \\
l + m &= n
\end{aligned}
\end{equation}

\[ \begin{equation} \begin{aligned} a &= b + c \\ d &= e + f + g \\ h + i &= j + k \\ l + m &= n \end{aligned} \end{equation} \]

\(\texttt{split}\) 环境和 \(\texttt{aligned}\) 环境用法类似，也用于和 \(\texttt{equation}\) 环境套用，区别是 \(\texttt{split}\) 只能将每行的一个公式分两栏，\(\texttt{aligned}\) 允许每行多个公式多栏。

数组和矩阵

为了排版二维数组，\(\LaTeX{}\) 提供了 \(\texttt{array}\) 环境，用法与 \(\texttt{tabular}\) 环境极为类似，也需要定义列格式，并用 \\ 换行。数组可作为一个公式块，在外套用 \left、\right 等定界符：

1
2
3
4
5
6
7
\[ \mathbf{X} = \left(
\begin{array}{cccc}
x_{11} & x_{12} & \ldots & x_{1n}\\
x_{21} & x_{22} & \ldots & x_{2n}\\
\vdots & \vdots & \ddots & \vdots\\
x_{n1} & x_{n2} & \ldots & x_{nn}\\
\end{array} \right) \]

\[ \mathbf{X} = \left( \begin{array}{cccc} x_{11} & x_{12} & \ldots & x_{1n}\\ x_{21} & x_{22} & \ldots & x_{2n}\\ \vdots & \vdots & \ddots & \vdots\\ x_{n1} & x_{n2} & \ldots & x_{nn}\\ \end{array} \right) \]

值得注意的是，上一节末尾介绍的 \(\texttt{aligned}\) 等环境也可以用定界符包裹。

还可以利用空的定界符排版出这样的效果：

1
2
3
4
5
6
\[ |x| = \left\{
\begin{array}{rl}
-x & \text{if } x < 0,\\
0 & \text{if } x = 0,\\
x & \text{if } x > 0.
\end{array} \right. \]

\[ |x| = \left\{ \begin{array}{rl} -x & \text{if } x < 0,\\ 0 & \text{if } x = 0,\\ x & \text{if } x > 0. \end{array} \right. \]

不过上述例子可以用 amsmath 提供的 \(\texttt{cases}\) 环境更轻松地完成：

1
2
3
4
5
6
\[ |x| =
\begin{cases}
-x & \text{if } x < 0,\\
0 & \text{if } x = 0,\\
x & \text{if } x > 0.
\end{cases} \]

\[ |x| = \begin{cases} -x & \text{if } x < 0,\\ 0 & \text{if } x = 0,\\ x & \text{if } x > 0. \end{cases} \]

amsmath 宏包还直接提供多种排版矩阵的环境，包括不带定界符的 \(\texttt{matrix}\)，以及带各种定界符的矩阵 \(\texttt{pmatrix}\)（\(\bigl(\)）、\(\texttt{bmatrix}\)（\(\bigl[\)）、\(\texttt{Bmatrix}\)（\(\bigl\{\)）、\(\texttt{vmatrix}\)（\(\bigl\vert\)）、\(\texttt{Vmatrix}\)（\(\bigl\Vert\)）。使用这些环境时，无需给定列格式（事实上这些矩阵内部也是用 \(\texttt{array}\) 环境生成的。）

1
2
3
4
5
6
7
8
9
10
11
\[
\begin{matrix}
1 & 2 \\ 3 & 4
\end{matrix} \qquad
\begin{bmatrix}
x_{11} & x_{12} & \ldots & x_{1n}\\
x_{21} & x_{22} & \ldots & x_{2n}\\
\vdots & \vdots & \ddots & \vdots\\
x_{n1} & x_{n2} & \ldots & x_{nn}\\
\end{bmatrix}
\]

\[ \begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix} \qquad \begin{bmatrix} x_{11} & x_{12} & \ldots & x_{1n}\\ x_{21} & x_{22} & \ldots & x_{2n}\\ \vdots & \vdots & \ddots & \vdots\\ x_{n1} & x_{n2} & \ldots & x_{nn}\\ \end{bmatrix} \]

在矩阵中的元素里排版分式时，要用到\dfrac 等命令：

1
2
3
4
5
6
7
8
9
10
11
\[
\mathbf{H}=
\begin{bmatrix}
\dfrac{\partial^2 f}{\partial x^2} &
\dfrac{\partial^2 f}
      {\partial x \partial y} \\[8pt]
\dfrac{\partial^2 f}
      {\partial x \partial y} &
\dfrac{\partial^2 f}{\partial y^2}
\end{bmatrix}
\]

\[ \mathbf{H}= \begin{bmatrix} \dfrac{\partial^2 f}{\partial x^2} & \dfrac{\partial^2 f} {\partial x \partial y} \\[8pt] \dfrac{\partial^2 f} {\partial x \partial y} & \dfrac{\partial^2 f}{\partial y^2} \end{bmatrix} \]

公式中的间距

绝大部分时候，数学公式中各元素的间距是根据符号类型自动生成的，需要手动调整的情况极少。已经认识了两个生成间距的命令 \quad 和 \qquad。在公式中可能用到的间距还包括\,、\:、\; 以及负间距 \!。文本中的 \␣ 也能使用在数学公式中。

image-20250120153652472

一个常见的用途是修正积分的被积函数 \(f(x)\) 和微元 \(\mathrm{d}x\) 之间的距离。注意微元里的 \(\mathrm{d}\) 用的是直立体：

1
2
3
4
5
\[
\int_a^b f(x)\mathrm{d}x
\qquad
\int_a^b f(x)\,\mathrm{d}x
\]

\[ \int_a^b f(x)\mathrm{d}x \qquad \int_a^b f(x)\,\mathrm{d}x \]

另一个用途是生成多重积分号。如果直接连写两个 \int，之间的间距将会过宽，此时可以使用负间距 \! 修正之。不过 amsmath 提供了更方便的多重积分号，如二重积分 \iint、三重积分\iiint 等。

1
2
3
4
5
6
7
\newcommand\diff{\,\mathrm{d}}
\begin{gather*}
\int\int f(x)g(y) \diff x \diff y \\
\int\!\!\!\int f(x)g(y) \diff x \diff y \\
\iint f(x)g(y) \diff x \diff y \\
\iint\quad \iiint\quad \idotsint
\end{gather*}

\[ \newcommand\diff{\,\mathrm{d}} \begin{gather*} \int\int f(x)g(y) \diff x \diff y \\ \int\!\!\!\int f(x)g(y) \diff x \diff y \\ \iint f(x)g(y) \diff x \diff y \\ \iint\quad \iiint\quad \idotsint \end{gather*} \]

数学符号的字体控制

数学字母字体

\(\LaTeX{}\) 允许一部分数学符号切换字体，主要是拉丁字母、数字、大写希腊字母以及重音符号等。下表给出了切换字体的命令。某些命令需要字体宏包支持。

1
2
3
4
% \usepackage{amssymb}
$\mathcal{R} \quad \mathfrak{R} \quad \mathbb{R}$
\[\mathcal{L} = -\frac{1}{4}F_{\mu\nu}F^{\mu\nu}\]
$\mathfrak{su}(2)$ and $\mathfrak{so}(3)$ Lie algebra

\[ % \usepackage{amssymb} \begin{gather*} \mathcal{R} \quad \mathfrak{R} \quad \mathbb{R} \\ \mathcal{L} = -\frac{1}{4}F_{\mu\nu}F^{\mu\nu} \\ \mathfrak{su}(2) \ and \ \mathfrak{so}(3) \ Lie \ algebra \end{gather*} \]

image-20250120160607188

一般来说，不同的数学字体往往带有不同的语义，如矩阵、向量等常会使用粗体或粗斜体，而数集常会使用 \mathbb 表示。出于内容与格式分离以及方便书写的考虑，可以为它们定义新的命令。

加粗的数学符号

上表中的 \mathbf 命令只能获得直立、加粗的字母。如果想得到粗斜体（国内使用粗斜体符号表示矢量，见 GB/T 3102.11—1993）。可以使用 amsmath 宏包提供的 \boldsymbol 命令：

1
$\mu, M \qquad \boldsymbol{\mu}, \boldsymbol{M}$

\[ \mu, M \qquad \boldsymbol{\mu}, \boldsymbol{M} \]

也可以使用 bm 宏包提供的 \bm 命令：

1
2
% \usepackage{bm}
$\mu, M \qquad \bm{\mu}, \bm{M}$

在 \(\LaTeX{}\) 默认的数学字体中，一些符号本身并没有粗体版本，使用 \boldsymbol 也得不到粗体。此时 \bm 命令会生成“伪粗体”，尽管效果比较粗糙，但在某些时候也不失为一种解决方案。

数学符号的尺寸

数学符号按照符号排版的位置规定尺寸，从大到小包括行间公式尺寸、行内公式尺寸、上下标尺寸、次级上下标尺寸。除了字号有别之外，行间和行内公式尺寸下的巨算符也使用不一样的大小。 为每个数学尺寸指定了一个切换的命令，见 下表。

命令 尺寸 示例
\displaystyle 行间公式尺寸 \(\displaystyle\sum a\)
\textstyle 行内公式尺寸 \(\textstyle\sum a\)
\scriptstyle 上下标尺寸 \(\scriptstyle a\)
\scriptscriptstyle 次级上下标尺寸 \(\scriptscriptstyle a\)

通过以下示例对比行间公式和行内公式的区别。在分式中，分子分母默认为行内公式尺寸，示例中将分母切换到行间公式尺寸：

1
2
3
4
5
6
7
8
\[
r = \frac
  {\sum_{i=1}^n (x_i- x)(y_i- y)}
  {\displaystyle \left[
    \sum_{i=1}^n (x_i-x)^2
    \sum_{i=1}^n (y_i-y)^2
  \right]^{1/2} }
\]

\[ r = \frac {\sum_{i=1}^n (x_i- x)(y_i- y)} {\displaystyle \left[ \sum_{i=1}^n (x_i-x)^2 \sum_{i=1}^n (y_i-y)^2 \right]^{1/2} } \]

定理环境

\(\LaTeX{}\) 原始的定理环境

使用 \(\LaTeX{}\) 排版数学和其他科技文档时，会接触到大量的定理、证明等内容。\(\LaTeX{}\) 提供了一个基本的命令 \newtheorem 提供定理环境的定义：

1
2
\newtheorem{theorem environment}{title}[section-level] \\
\newtheorem{theorem environment}[counter]{title}

\(\textrm{theorem environment}\) 为定理环境的名称。原始的 \(\LaTeX{}\) 里没有现成的定理环境，不加定义而直接使用很可能会出错。\(\textrm{title}\) 是定理环境的标题（“定理”，“公理”等）。

定理的序号由两个可选参数之一决定，它们不能同时使用：

  • \(\textrm{section-level}\) 为章节级别，如 \(\texttt{chapter}\)、\(\texttt{section}\) 等，定理序号成为章节的下一级序号；
  • \(\textrm{counter}\) 为用 \newcounter 自定义的计数器名称，定理序号由这个计数器管理。

如果两个可选参数都不用的话，则使用默认的与定理环境同名的计数器。

在以下示例代码中，定义了一个 \(\texttt{mythm}\) 环境，其序号设为 \(\texttt{section}\) 的下一级序号。注意 \(\texttt{mythm}\) 环境的可选参数以及 \label 的用法：

1
2
3
4
5
6
7
8
9
10
11
12
\newtheorem{mythm}{My Theorem}[section]
\begin{mythm}\label{thm:light}
The light speed in vacuum
is $299,792,458\,\mathrm{m/s}$.
\end{mythm}
\begin{mythm}[Energy-momentum relation]
The relationship of energy,
momentum and mass is
\[E^2 = m_0^2 c^4 + p^2 c^2\]
where $c$ is the light speed
described in theorem \ref{thm:light}.
\end{mythm}

image-20250120165121095

amsthm 宏包

\(\LaTeX{}\) 默认的定理环境格式为粗体标签、斜体内容、定理名用小括号包裹。如果需要修改格式，则要依赖其它的宏包，如 amsthm、ntheorem 等等。本小节简单介绍一下 amsthm 的用法。

amsthm 提供了 \theoremstyle 命令支持定理格式的切换，在用 \newtheorem 命令定义定理环境之前使用。amsthm 预定义了三种格式用于\theoremstyle：\(\texttt{plain}\) 和 \(\LaTeX{}\) 原始的格式一致；\(\texttt{definition}\) 使用粗体标签、正体内容；\(\texttt{remark}\) 使用斜体标签、正体内容。

另外 amsthm 还支持用带星号的 \newtheorem* 定义不带序号的定理环境：

1
2
3
\theoremstyle{definition} \newtheorem{law}{Law}
\theoremstyle{plain} \newtheorem{jury}[law]{Jury}
\theoremstyle{remark} \newtheorem*{mar}{Margaret}

以上例子定义的 \(\texttt{jury}\) 环境与 \(\texttt{law}\) 环境共用编号，\(\texttt{mar}\) 环境不编号：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
\theoremstyle{definition} \newtheorem{law}{Law}
\theoremstyle{plain} \newtheorem{jury}[law]{Jury}
\theoremstyle{remark} \newtheorem*{mar}{Margaret}
\begin{law}\label{law:box}
Don't hide in the witness box.
\end{law}
\begin{jury}[The Twelve]
It could be you! So beware and
see law~\ref{law:box}.\end{jury}
\begin{jury}
You will disregard the last
statement.\end{jury}
\begin{mar}No, No, No\end{mar}
\begin{mar}Denis!\end{mar}

image-20250120171711806

amsthm 还支持使用 \newtheoremstyle 命令自定义定理格式，更为方便使用的是 ntheorem 宏包。感兴趣的读者可参阅它们的帮助文档。

证明环境和证毕符号

amsthm 还提供了一个 \(\texttt{proof}\) 环境用于排版定理的证明过程。环境末尾自动加上一个 □ 证毕符号：

1
2
3
4
5
6
7
\begin{proof}
For simplicity, we use
\[
E=mc^2
\]
That's it.
\end{proof}

image-20250120173549574

如果行末是一个不带编号的公式，□ 符号会另起一行，这时可使用 \qedhere 命令将 □ 符号放在公式末尾：

image-20250120173828551

\qedhere 对于 \(\texttt{align*}\) 等环境也有效：

1
2
3
4
5
6
7
8
\begin{proof}
Assuming $\gamma
= 1/\sqrt{1-v^2/c^2}$, then
\begin{align*}
E &= \gamma m_0 c^2  \\
p &= \gamma m_0v \qedhere
\end{align*}
\end{proof}

image-20250120174116569

在使用带编号的公式时，最好不要在公式末尾使用 \qedhere 命令。对带编号的公式使用\qedhere 命令会使 □ 符号放在一个难看的位置，紧贴着公式：

image-20250120174348875

在 \(\texttt{align}\) 等环境中使用 \qedhere 命令会使 □ 盖掉公式的编号；使用 \(\texttt{equation}\) 嵌套 \(\texttt{aligned}\) 等环境时，\qedhere 命令会将 □ 直接放在公式后。这些位置都不太正常。

证毕符号 □ 本身被定义在命令 \qedsymbol 中，如果有使用实心符号作为证毕符号的需求，需要自行用 \renewcommand}命令修改。可以利用标尺盒子来生成一个适当大小的“实心矩形”：

1
2
3
4
5
6
7
8
\renewcommand{\qedsymbol}%
  {\rule{1ex}{1.5ex}}
\begin{proof}
For simplicity, we use
\[
E=mc^2 \qedhere
\]
\end{proof}

image-20250120174901879

符号表

在这里。

参考文献

[1] Partl H, Hyna I, Schlegl E. 一份 (不太) 简短的 LATEX2ε 介绍[J]. 2024. https://github.com/CTeX-org/lshort-zh-cn